Aim of the workThe dynamics of multiple interacting species is often complex and the consequences of perturbation of large ecosystems are difficult to predict. Mathematical modeling gives insights on the structure-stability-dynamics relationships and help to interpret experimental observations.The aim of this work is to simulate the generalized Lotka-Volterra (gLV) model and to analyze some dynamical properties of multi-species systems. The multi-species Lotka-Volterra modelThe generalized Lotka-Volterra (gLV) model simulates the time evolution of a multi-species system: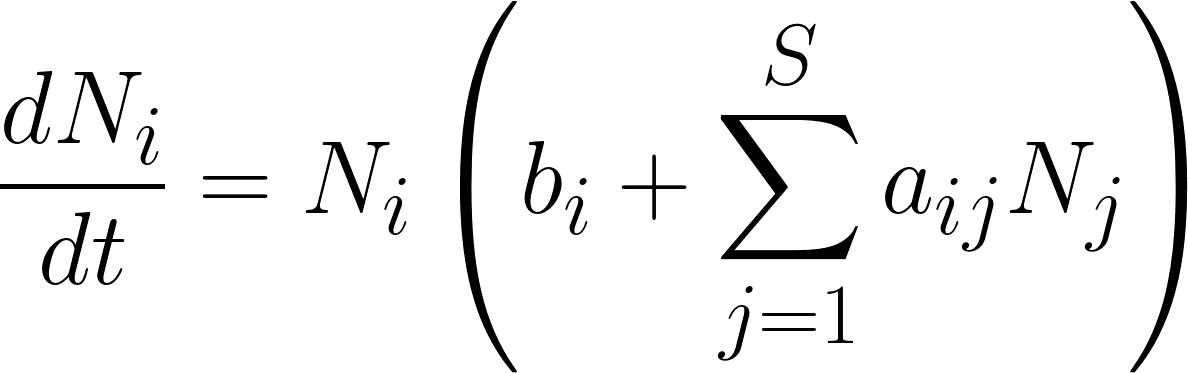 What do the parameters bi and aij represent? The above equation can be rewritten in matricial form: Write matrix A for the following microbial network: 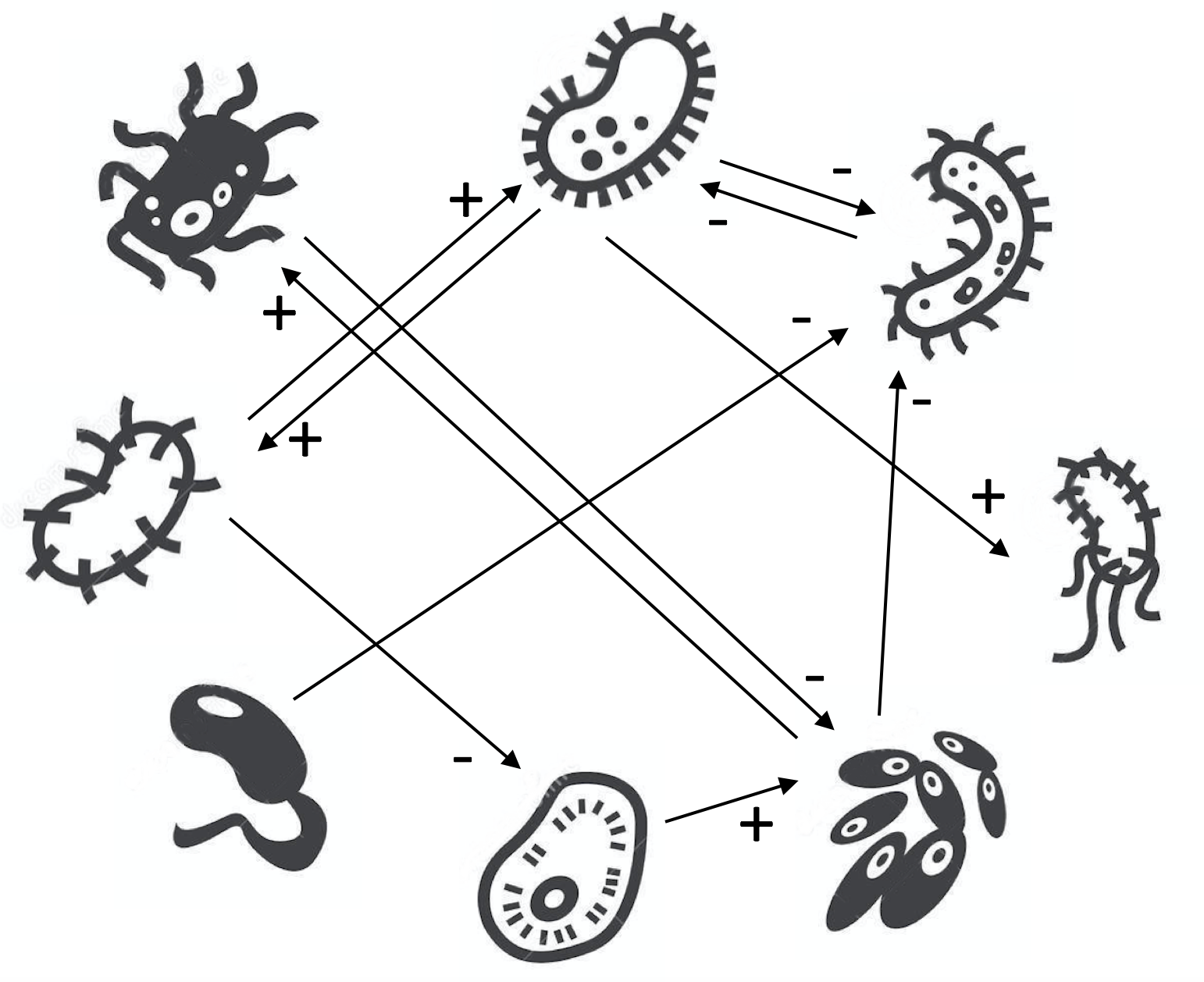 How does the matrix A look like for trophic food web (such as the one depicted on this figure)? How could we theoretically calculate the steady state of the system? What it the potential problem with this calculation? Simulation of the gLV modelRun simulations of the gLV model and discuss the effect of model parameters (number of species N, type and connectance of the interaction matrix, initial abundance, etc).Species number vs survival rateAs you may have seen in your previous simulations, some species tends to die. Are bigger populations (i.e. population involving more species) more susceptible to species loss? To test this, you can compute and plot the survival rate as a function of the number of species. How do the type and connectance of the interaction matrix affect the observed tendancy. How does the positive vs negative interaction ratio influence the results?Wigner-May theoremThe above results suggest that stability is associated with complexity. Much work has been done to characterize these relationships and to identify the ecological factors that affect population stability. One key theoretical results, reported by May (1972) and known as the Wigner-May relationship, is the following: Using the gLV equations, May analyzed the probability P(S,α,C) for a system composed of S species with connectivity C (with 0 < C < 1) to be stable. For an interaction matrix A where the elements are drawn from a Normal distribution with mean 0 and standard deviation α, May established that:Rather that to check the above relationship, we propose here to compute the survival rate as a function of S and C for various values of α. ChaosChaos can be generated by coupling oscillatory systems. Show that chaos can be obtained in a mutually coupled predator-prey systems: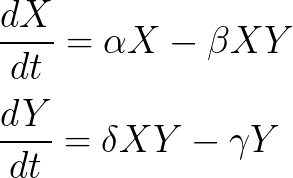 This can be done in 2 steps: (1) Parametrize a 4-species system so that it correspond to 2 independent predator-prey systems. (2) Introduce a (small) coupling between the 2 systems. Chaos is characterized by its sensitivity to initial conditions. Run simulation from two close initial conditions and observe the divergence (decorrelation) of the trajectories (butterfly effect). MultistabilityThe coexistence of multiple stables steady states (=multistability) can be illustrated with a variant of the Lotka-Volterra model in which the growth rates are described by "inhibitory" Hill function: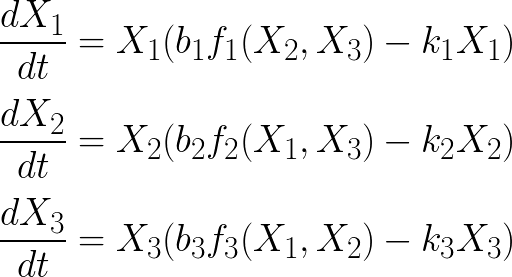
 In this 3-species system, the growth of each species is inhibited by the two others. For the present practicals we will limit our analysis to this toy model but it can easily be generalized to N species. Simulate this system for the following parameter values and for various initial conditions, and show the existence of tristability: Kij = 0.1 ∀ i = j, n = 2, and ki = 0.1 ∀ i, b1 = 1, b2 = 0.95, b3 = 1.05. Switches from one stable state to another can be induced by a transient change of a parameter value. Show that increasing b1 for a certain duration lead to a switch. What is the minimum value of b1 to observe the switch (tipping point)? How to induce the opposite switch? This illustrates the hysteresis effect. References
|